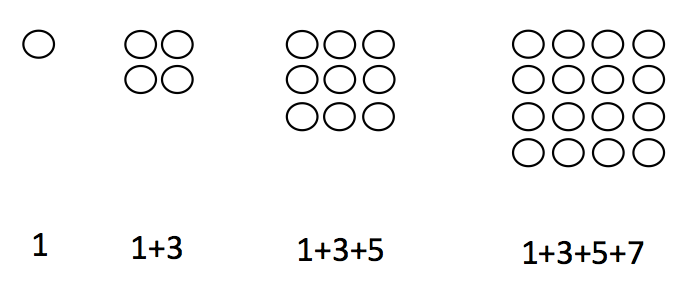Introduction to calculus

Calculus (from Latin calculus, literally "small pebble used for counting on an abacus")is the mathematical study of continuous change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus(concerning rates of change and slopes of curves),and integral calculus (concerning accumulation of quantities and the areas under and between curves); these two branches are related to each other by thefundamental theorem of calculus. Both branches make use of the fundamental notions of convergence of infinite sequencesand infinite series to a well-defined limit. Generally, modern calculus is considered to have been developed in the 17th century byIsaac Newton and Gottfried Leibniz. Today, calculus has widespread uses in science,engineering and economics.

Calculus is a part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study offunctions and limits, broadly calledmathematical analysis. Calculus has historically been called "the calculus ofinfinitesimals", or "infinitesimal calculus".Calculus (plural calculi) is also used for naming some methods of calculation or theories of computation, such aspropositional calculus, calculus of variations,lambda calculus, and process calculus.

Plane analytical geometry

Plane Analytical Geometry

By M Bourne

The curves that we learn about in this chapter are called conic sections. They arise naturally in many situations and are the result of slicing a cone at various angles.

Depending on where we slice our cone, and at what angle, we will either have a straight line, a circle, a parabola, an ellipse or a hyperbola. Of course, we could also get a single point, too.

An interesting application from nature:

Why study analytic geometry?

Science and engineering involves the study of quantities that change relative to each other (for example, distance-time, velocity-time, population-time, force-distance, etc).

It is much easier to understand what is going on in these problems if we draw graphs showing the relationship between the quantities involved.

The study of calculus depends heavily on a clear understanding of functions, graphs, slopes of curves and shapes of curves. For example, in the Differentiation chapter we use graphs to demonstrate relationships between varying quantities.

We begin with some basic definitions of slope, parallel lines and perpendicular lines.

cylinder facts

Cylinder Facts

Notice these interesting things:

• It has a flat base and a
  flat top
• The base is the same as the top
• From base to top the shape stays the same
• It has one curved side
• It is not a polyhedron as it has a curved surface

An object shaped like a cylinder is said to be cylindrical.

Surface Area of a Cylinder

Surface Area = 2 × π × r × (r+h)

Which is made up of:

• Surface Area of One End = π × r²
• Surface Area of Side = 2 × π × r × h

Example: h = 7 and r = 2

Surface Area		= 2 × π × r × (r+h)
		= 2 × π × 2 × (2+7)
		= 2 × π × 2 × 9
		= 36 π
		≈ 113.097

Volume of a Cylinder

Volume = π × r² × h

Just multiply the area of the base by the height of the cylinder:

• Area of the base: π × r²
• Height: h
• Volume = Area × Height = π × r² × h

Example: h = 7 and r = 2

Volume		= π × r2 × h
		= π × 22 × 7
		= 28 π
		≈  87.96

How to remember: Volume = pizza

Imagine you just cooked a pizza.
The radius is "z", and the thickness "a" is the same everywhere ... what is the volume?

Volume equals   pi × z × z × a

(we would normally write "pi" as π, and z × z as z², but you get the idea!)

Volume of a Cone vs Cylinder

The volume formulas for cylinders and cones are very similar:

The volume of a cylinder is:	π × r2 × h
The volume of a cone is:	1 3 π × r2 × h

So a cone's volume is exactly one third ( 1 3 ) of a cylinder's volume.
In future, order your ice creams in cylinders, not cones, you get 3 times as much!

It Doesn't Have to Be Circular

Usually when we say Cylinder we mean a Circular Cylinder, but you can also have Elliptical Cylinders, like this one:

And we can have stranger cylinders!
So long as the cross-section is curved and is the same from one end to the other, then it is a cylinder. But the area and volume calculations will be different than for the above.

More Cylinders

facts about torus

Torus Facts

Notice these interesting things:

• It can be made by revolving a
  small circle (radius r) along a line made
  by a bigger circle (radius R).
• It has no edges or vertices
• It is not a polyhedron

Torus in the Sky.
The Torus is such a beautiful solid,
this one would be fun at the beach !

Surface Area

Surface Area = 4 × π² × R × r

Example: r = 3 and R = 7

Surface Area		= 4 × π2 × R × r
		= 4 × π2 × 7 × 3
		= 4 × π2 × 21
		= 84 × π2
		≈ 829

Volume

Volume = 2 × π² × R × r²

Example: r = 3 and R = 7

Volume		= 2 × π2 × R × r2
		= 2 × π2 × 7 × 32
		= 2 × π2 × 7 × 9
		= 126 π2
		≈ 1244

Note: Area and volume formulas only work when the torus has a hole!

And did you know that Torus was the Latin word for a cushion? (This is not a real roman cushion, just an illustration I made)

When we have more than one torus they are called tori
 

As the small radius (r) gets larger and larger, the torus goes from looking like a Tire to a Donut:

shapes

Cube	Cubes have 6 faces, 12 edges and 8 vertices. All sides on a cube are equal length. All faces are square in shape. A cube is a type of cuboid.
Cuboid	Cuboids have 6 faces, 12 edges and 8 vertices. All the faces on a cuboid are rectangular.
Sphere	Spheres have either 0 or 1 faces, 0 edges and 0 vertices.
Cylinder	Cylinders have either 2 or 3 faces, 0 or 2 edges, and 0 vertices.
Cone	Cones have either 1 or 2 faces, 0 or 1 edges, and 1 apex (which is described by some mathematicians as a vertex).
Triangular Prism	Triangular Prisms have 5 faces, 9 edges, and 6 vertices. The two faces at either end are triangles, and the rest of the faces are rectangular.
Hexagonal Prism	Hexagonal Prisms have 8 faces, 18 edges, and 12 vertices. The two faces at either end are hexagons, and the rest of the faces are rectangular.
Triangular-based Pyramid	Triangular-based pyramids have 4 faces, 6 edges and 4 vertices. The base is a triangle. All of the faces are triangular. If the triangular faces making up the prism are all equilateral, then the shape is also called a Tetrahedron.
Square-based Pyramid	Square based pyramids have 5 faces, 8 edges and 5 vertices The base is a square. All the other faces are triangular.
Hexagonal Pyramid	Hexagonal pyramids have 7 faces, 12 edges, and 7 vertices. The base is a hexagon. All of the other faces are triangular.

Applications of matrices

Practical Uses of Matrix Mathematics

December 17, 2013 by Mike DeHaan 46 Comments

Share28

+17

Share3

Pin

Tweet

SHARES38

What are the practical use of matrices in day to day life? Image by Lakeworks.

My thanks to an alert reader for asking, “What are the practical use of matrices in day to day life?” The most direct answer is, “It depends on your own day to day life.” Let’s consider some practical uses of matrix mathematics in a variety of settings, along with a brief introduction to matrices.

Applications of Matrix Mathematics

Matrix mathematics applies to several branches of science, as well as different mathematical disciplines. Let’s start with computer graphics, then touch on science, and return to mathematics.

We see the results of matrix mathematics in every computer-generated image that has a reflection, or distortion effects such as light passing through rippling water.

Before computer graphics, the science of optics used matrix mathematics to account for reflection and for refraction.

Matrix arithmetic helps us calculate the electrical properties of a circuit, with voltage, amperage, resistance, etc.

In mathematics, one application of matrix notation supports graph theory. In an adjacency matrix, the integer values of each element indicates how many connections a particular node has.

The field of probability and statistics may use matrix representations. A probability vector lists the probabilities of different outcomes of one trial. A stochastic matrix is a square matrix whose rows are probability vectors. Computers run Markov simulations based on stochastic matrices in order to model events ranging from gambling through weather forecasting to quantum mechanics.

Matrix mathematics simplifies linear algebra, at least in providing a more compact way to deal with groups of equations in linear algebra.

Introduction to Matrix Arithmetic

A matrix organizes a group of numbers, or variables, with specific rules of arithmetic. It is represented as a rectangular group of rows and columns, such as . This “2X3” matrix has two rows and three columns; the number ’23’ is in the second row of the third column.

An example of a square matrix with variables, rather than numbers, is . This is a square matrix because the number of rows equals the number of columns.

We can only add matrices of the same dimensions, because we add the corresponding elements. .

Matrix multiplication is another matter entirely. Let’s multiply matrices MP=R. M is an mXn matrix; P is nXp; and the result R will have dimension mXp. Note that the number of columns of the left-hand matrix, M, must equal the number of rows of the right hand matrix, P. For example:

.

A matrix can also multiply, or be multiplied by, a vector.

Surprisingly, we all use matrix in our daily lives. Image by Kkmann.

Graphic Uses of Matrix Mathematics

Graphic software uses matrix mathematics to process linear transformations to render images. A square matrix, one with exactly as many rows as columns, can represent a linear transformation of a geometric object. For example, in the Cartesian X-Y plane, the matrix  reflects an object in the vertical Y axis. In a video game, this would render the upside-down mirror image of a castle reflected in a lake.

If the video game has curved reflecting surfaces, such as a shiny silver goblet, the linear transformation matrix would be more complicated, to stretch or shrink the reflection.

The Identity Matrix and the Inverse Matrix

The Identity matrix is an nXn square matrix with ones on the diagonal and zeroes elsewhere. It causes absolutely no change as a linear transformation; much like multiplying an ordinary number by one. The dimension of an Identity matrix is shown by a subscript, so I₂ =  is the 2X2 Identity matrix.

Suppose we have two square nXn matrices, A and B, such that AB=I_n. Then we call B the inverse matrix of A, and show it as A^-1. The first practical point is that the inverse matrix A^-1 reverses the changes made by the original linear transformation matrix A.

The Determinant

Another important task in matrix arithmetic is to calculate the determinant of a 2X2 square matrix. For matrix M= , the determinant is |M| = a*d – b*c.

If the determinant of M is zero, then no inverse matrix M^-1 exists.

On the other hand, if we apply M as the linear transformation of a unit square U into U_M, then the determinant |M| is the area of that transformed square. In a sense, the determinant is the size, or “norm”, of a square matrix.

Daily Matrix Applications

Matrix mathematics has many applications. Mathematicians, scientists and engineers represent groups of equations as matrices; then they have a systematic way of doing the math. Computers have embedded matrix arithmetic in graphic processing algorithms, especially to render reflection and refraction. Some properties of matrix mathematics are important in math theory.

However, few of us are likely to consciously apply matrix mathematics in our day to day lives.

Beauty of mathematics

THE BEAUTY OF MATHEMATICS

For many people, memories of maths lessons at school are anything but pretty. Yet “beautiful” is a word that I and other mathematicians often use to describe our subject. How on earth can maths be beautiful—and does it matter?

Win an iPhone 7 Sign up to our daily newsletter for your chance to win.

For me, as a mathematician, it is hugely important. My enjoyment of the beauty of mathematics is part of what motivates me to study the subject. It is also a guide when I am working on a problem: If I think of a few strategies, I will choose the one that seems most elegant first. And if my solution seems clumsy then I will revisit it to try to make it more attractive.

I’ve just finished marking a pile of homework from my second-year mathematics undergraduates. I am struck by two students’ contrasting solutions to one problem. Both solutions are correct, both answer the question. And yet I much prefer one to the other. It’s not just that one is longer than the other, or that one is explained better than the other (both are described well, in fact.)

The longer one doesn’t quite get to the heart of the matter, it’s a bit cluttered with unnecessary distractions. The other uses a different approach, that captures the essence of the ideas—it helps the reader to understandwhy this piece of mathematics works this way, not just that it does. For a mathematician, the “why” is critical, and we are always looking for arguments that reveal this.

Some cases of mathematical beauty are clear. Fractals, for example, are mathematical sets of numbers—corresponding to shapes—that have striking self-similarity and that have inspired numerous artists.

Less is more

But what about less obvious cases? Let me try to give you an example. Perhaps you recognize the sequence of numbers 1, 3, 6, 10, 15, 21, 28, … This is a sequence that students often encounter at school: the triangular numbers. Each number in the sequence corresponds to the number of dots in a sequence of triangles.

The six first triangular numbers: 1, 3, 6, 10, 15, 21.

Can we predict what the 1000th number in the sequence will be? There are many ways to tackle this question, and in fact unpicking the similarities and differences between these approaches is in itself both mathematical and enlightening. But here is one rather beautiful argument.

Imagine the 10th number in the sequence (because it’s easier to draw the picture than for the 1000th!) Let’s count the dots without counting the dots. We have a triangle of dots, with 10 in the bottom row and 10 rows of dots.

If we make another copy of that arrangement, we can rotate it and put it next to our original triangle of dots—so that the two triangles form a rectangle. This shape of dots will have 10 in the bottom row and 11 rows, so there are 10 x 11 = 110 dots in total (see figure below.) Now we know that half of those were in our original triangle, so the 10th triangular number is 110/2 = 55. And we didn’t have to count them.

The 10th triangular number x2.

The power of this mathematical argument is that we can painlessly generalize to any number—even without drawing the dots. We can do a thought experiment. The 1000th triangle in the sequence will have 1000 dots in the bottom row, and 1000 rows of dots. By making another copy of this and rotating it, we get a rectangle with 1000 dots in the bottom row and 1001 rows. Half of those dots were in the original triangle, so the 1000th triangular number is (1000 x 1001)/2 = 500500.

For me, this idea of drawing the dots, duplicating, rotating and making a rectangle is beautiful. The argument is powerful, it generalizes neatly (to any size of triangle,) and it reveals why the answer is what it is.

There are other ways to predict this number. One is to look at the first few terms of the sequence, guess a formula, and then prove that the formula does work (for example by using a technique called proof by induction.) But that doesn’t convey the same memorable explanation behind the formula. There is an economy to the argument with pictures of dots, a single diagram captures everything we need to know.

Here’s another argument that I find attractive. Let’s think about the sum below:

The harmonic series.

This is the famous harmonic series. It turns out that it doesn’t equal a finite number—mathematicians say that the sum “diverges.” How can we prove that? It sounds difficult, but one elegant idea does the job.

The harmonic series with grouped terms.

Here each group of fractions adds up to more than ½. We know that ⅓ is bigger than ¼. That means (⅓) + (¼) is bigger than (¼) + (¼), which equals ½. So by adding enough blocks, each bigger than ½, the sum gets bigger and bigger—we can beat any target we like. By adding an infinite number of them we will get an infinite sum. We have tamed the infinite, with a beautiful argument.

A waiting game?

These are not the most difficult pieces of mathematics. One of the challenges of mathematics is that tackling more sophisticated problems often means first tackling more sophisticated terminology and notation. I cannot find a piece of mathematics beautiful unless I first understand it properly—and that means it can take a while for me to appreciate the aesthetic qualities.

I don’t think this unique to mathematics. There are pieces of music, buildings, pieces of visual art where I have not at first appreciated their beauty or elegance—and it is only by persevering, by grappling with the ideas, that I have come to perceive the beauty.

For me, one of the joys of teaching undergraduates is watching them develop their own appreciation of the beauty of mathematics. I’m going to see my second years this afternoon to go over their homework, and I already know that we’re going to have an interesting conversation about their different solutions—and that considering the aesthetic qualities will play a part in deepening their understanding of the mathematics.

School students can have just the same experience: when they’re given the opportunity to engage with rich questions, when they can play with mathematical ideas, when they have the chance to experience multiple strategies to the same question rather than just getting the answer in the back of the textbook and moving on. The mathematical ideas do not have to be university level, there are beautiful problems that are perfect for school students. Happily, there are many math teachers and math education projects that are helping students to have those experiences of the beauty of mathematics.

Discover the mathematician within you

Discover the mathematician within you with this simple problem

The power of multiple representations

I could never do music. I never learned to play an instrument, not a lick. I had no clue how a musical score is crafted. A music sheet was no more intelligible to me than a foreign language. So while I could appreciate classical music on a superficial level as a listener, understanding it was for other people.

That all changed five years ago in grad school when a professor introduced us toMusic Animation Machine — Stephen Malinowski’s animated graphical score project. I watched with dumb-struck awe as the professor played a clip of Bach’s Toccata and Fugue in D minor. The piece was no different to usual, except that it was brought to life with the most intuitive of visualisations. I needed no training in obscure symbols or terms to make sense of Bach. The subtleties of pitch and rhythm were revealed with the simplest of coloured bar representations. I could identify and even anticipate recurring patterns. I heard notes that had previously eluded me.

Bach as you’ve never seen him

In that moment, a new thought took hold of me. A deep understanding of music was within my grasp after all. A virtuoso I was not, but for the first time in my life, I was able to truly connect with classical music. It had only taken twenty-seven years, and an inspired presentation that defied everything I had been taught about music at school.

We need to do for maths what Stepehen Malinowski has done for classical music — place it within the reach of everyone, and especially those who have long given up on connecting with the beauty and elegance of the subject; even its simplicity.

Take the following problem, inspired byJames Tanton’s “Math without words” project:

Sum the first 100 odd integers.

No biggie — anyone and their calculator can knock this out with dogged effort. But that’s ninety-nine separate calculations; life’s too short for this brand of mathematics.

You may be tempted to impose theformula for summing an arithmetic series. But that hardly seems satisfying (and, after all, the formula did not just spring into being).

Let’s instead sum the first few terms, just to see what happens. However flaky it may seem, that strategy is perfectly natural to mathematicians. The key is to keep an open mind and to stay alert to any patterns. So:

1

1+3 = 4

1+ 3+ 5 = 9

1+ 3 + 5+ 7 = 16

Notice anything? The resulting values — 1,4,9,16 — may seem familiar. You will recall that they are the square numbers.

Hold up. We were just adding odd numbers — who invited squares to the party? Well, here they are. And we must now ask the question pursed on the lips of every mathematician.

Why?

Why does adding odd integers give us squares? Let’s find out. We can stare long and hard at the symbols above, but inspiration may not come unless we change the representation. Well, there’s a reason we call them square numbers — these values correspond to areas of squares! So

1 = 1 x 1

4 = 2 x 2

9 = 3 x 3

16= 4 x 4

and so on. That’s good, because we can now visualise this pattern to see what’s going on. We can draw the squares.

We can now literally see that summing the odd integers results in squares. The link between odds and squares is slowly revealing itself through this pictorial representation. You can sense the connection; why adding the next odd number gives the next square along. Perhaps you can’t quite put your finger on it.

So let’s go again, this time using a different colour in each step.

Amazing what a bit of colour can do, right? The connection is now clear — adding an odd integer corresponds to the next ‘layer’ of the square; that reverse L-shape. To get the next square along, we would need 5 along the bottom row, and a further four along the right-hand column, i.e. a total of 9 more spots.

So summing the first odd integers is no more and no less than the area of a 100x100 square. It’s ten thousand. But the answer is a mere side note to this problem. Consider what just happened — we started off with an arithmetic sum, represented by symbols on a page. We explored, we probed and we found a geometrical connection. We visualised the problem and saw the link for ourselves. We uncovered the geometry of odd numbers — we linked maths topics that are typically separated in the curriculum.

In short, we became mathematicians.

The lesson for educators — and the point of that graduate class — is to use multiple, diverse representations when presenting mathematical concepts.

Only a small minority of students will grasp the syntactic form of school maths. That does not make them any less capable; the limitation is one of curriculum and pedagogy.

As educators we are responsible for building as many entry points to understanding and engagement as we can. Visualisation alone is not a silver bullet; to understand and solve our problem, we needed to call on our core knowledge of odd numbers, basic addition and squares. But pictorial representation is a vital problem solving heuristic — mathematicians routinely translate abstract-sounding problems into visual ones. Visualisation is an equally vital — and engaging — way for students to undertake problem solving.

Mathematical thinking lies not in brute force calculation, but in shifting representations and finding connections. I hope this example persuades you (if you needed persuading) that a mathematician resides within you.

And with that, I invite you to explore this intriguing sum:

1 + 2 + 3 + … + 98 + 99 + 100 + 99 + 98 + 97 + … + 3 + 2 + 1

Enjoy.

Probability in real life

Examples of Real Life Probability

Probability in real life helps you make educated guesses.

Probability is the mathematical term for the likelihood that something will occur, such as drawing an ace from a deck of cards or picking a green piece of candy from a bag of assorted colors. You use probability in daily life to make decisions when you don't know for sure what the outcome will be. Most of the time, you won't perform actual probability problems, but you'll use [subjective probability](http://www.ehow.com/info_8526104_different-kinds-probability.html) to make judgment calls and determine the best course of action.

Planning Around the Weather

Nearly every day you use probability to plan around the weather. Meteorologists can't predict exactly what the weather will be, so they use tools and instruments to determine the likelihood that it will rain, snow or hail. For example, if there's a 60-percent chance of rain, then the weather conditions are such that 60 out of 100 days with similar conditions, it has rained. You may decide to wear closed-toed shoes rather than sandals or take an umbrella to work. Meteorologists also examine historical data bases to guesstimate high and low temperatures and probable weather patterns for that day or week.

Sports Strategies

Athletes and coaches use probability to determine the best sports strategies for games and competitions. A baseball coach evaluates a player's batting average when placing him in the lineup. For example, a player with a 200 batting average means he's gotten a base hit two out of every 10 at bats. A player with a 400 batting average is even more likely to get a hit -- four base hits out of every 10 at bats. Or, if a high-school football kicker makes nine out of 15 field goal attempts from over 40 yards during the season, he has a 60 percent chance of scoring on his next field goal attempt from that distance. The equation is:

9 / 15 = 0.60 or 60 percent

Insurance Options

Probability plays an important role in analyzing insurance policies to determine which plans are best for you or your family and what deductible amounts you need. For example, when choosing a car insurance policy, you use probability to determine how likely it is that you'll need to file a claim. For example, if 12 out of every 100 drivers -- or 12 percent of drivers -- in your community have hit a deer over the past year, you'll likely want to consider comprehensive -- not just liability -- insurance on your car. You might also consider a lower deductible if average car repairs after a deer-related incident run $2,800 and you don't have out-of-pocket funds to cover those expenses.

Games and Recreational Activities

You use probability when you play board, card or video games that involve luck or chance. You must weigh the odds of getting the cards you need in poker or the secret weapons you need in a video game. The likelihood of getting those cards or tokens will determine how much risk you're willing to take. For example, the odds are 46.3-to-1 that you'll get three of a kind in your poker hand -- approximately a 2-percent chance -- according to Wolfram Math World. But, the odds are approximately 1.4-to-1 or about 42 percent that you'll get one pair. Probability helps you assess what's at stake and determine how you want to play the game.

mathematics importance and uses

Mathematics: Meaning, Importance and Uses

Introduction: Mathematics is an indispensable subject of study. It plays an important role in forming the basis of all other sciences which deal with the material substance of space and time.

What is the meaning of Mathematics?

Mathematics may be described as the fundamental science. It is that branch of science that uses numbers and symbols. Numbers and symbols are arranged using systematic mathematical rules.

Mathematics may be broadly described as the science of space, time, measurement, quantities, shapes and numbers and their relationships with each other.

The study of mathematics is based on reasons. The universe exists in space and time, and is constituted of units of matter. To calculate the extension or composition of matter in space and time and to compute the units that make up the total mass of the material universe is the object of Mathematics. For the space-time quantum is everywhere full of matter and we have to know matter mathematically in the first instance.

Pure Mathematics vs. Applied Mathematics: Mathematics can be pure, i.e., the branch of science that deals that focuses on abstract concepts.

Pure mathematics is mainly concerned with concepts that are based on the rules of mathematics. Pure Mathematicians chiefly deal with establishing mathematical proofs. These concepts are not necessarily aimed at meeting the needs of the physical world.

Applied mathematics, on the other hand, is that branch of Mathematics that is applied to other branches such as chemistry, physics, chemistry, etc. It relies on a problem-solving approach. It tries to find a practical solutions to solve the day-to-day problems of life.

In practical world, pure mathematics and applied mathematics overlap each other. The concepts of pure mathematics are often used by applied mathematicians to find out practical solutions.

Importance of Mathematics

Knowledge of Mathematics is necessary for the study of the physical sciences.Computation and calculation are the basis of all studies that deal with matter in any form.Even the physician who has to study biological cells and bacilli need to have the knowledge of Mathematics, if he means to cut the margin of error which alone can make his diagnosis dependable.To the mechanic and the engineer it is a constant guide and help, and without exact knowledge of Mathematics, they cannot proceed one step in coming to grips with any complicated problem.Be it the airplane or the atom bomb, radio-communication or nuclear power, anything that has to do with anything concerning matter in any form, the knowledge of the principles of Mathematics is the one thing absolutely necessary.Mathematical calculations form an important role in architectural activities. Precise calculation are made while planning for the development of a new townships, buildings, bridges, etc.An elementary knowledge of the simplest branch of Mathematics, arithmetic, is the daily need of every man and woman in the ordinary affairs of life.

Intellectual Value of Mathematics

Mathematics has a most important bearing on the intellect as such. Study of Mathematics promotes habits of accuracy and exactitude, and prevents a man from being careless and slipshod.

It sharpens the reasoning powers of a man and increases his mental alertness.

On the whole a mathematically minded man is usually more dependable than one who is otherwise disposed. That is why the study of some Mathematics is compulsory up to the secondary stage of all education systems, and its habit has to be sedulously fostered.

Uses of Mathematics

Mathematics is very useful in our day-to-day life. It help us perform many of our tasks.

With basic mathematical skills, we can keep record of our day-to-day expenses.We can make budgets and preplan our expenditures. Budgeting is an important took to keep control over finances, especially expenditure.We can forecast sales and profit by applying mathematical tools.  Hence, it facilitates us to do business in an efficient way.We become more systematic in our approach while dealing with others.Mathematics facilitates business transactions. The value of purchases and sales are recorded using the principles of mathematics.Develop problem solving approach.Cooking: We need exact measure of vegetables, spices, flour, etc. while cooking food.A carpenter accurately measures the length and breadth of the wood and ply-board while making furniture.Basic mathematical calculations helps train and develop a child’s mind.

Conclusion

In the modern age, the intensely abstract nature of pure Mathematics has brought the science nearer to philosophy. Knowledge of Mathematics is indispensable both for the public person in the street as well as for scientists and philosophers.

Reference: important India.com