facts about torus

Torus Facts

Notice these interesting things: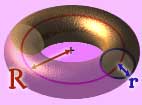

• It can be made by revolving a
  small circle (radius r) along a line made
  by a bigger circle (radius R).
• It has no edges or vertices
• It is not a polyhedron

Torus in the Sky.
The Torus is such a beautiful solid,
this one would be fun at the beach !

Surface Area

Surface Area = 4 × π² × R × r

Example: r = 3 and R = 7

Surface Area		= 4 × π2 × R × r
		= 4 × π2 × 7 × 3
		= 4 × π2 × 21
		= 84 × π2
		≈ 829

Volume

Volume = 2 × π² × R × r²

Example: r = 3 and R = 7

Volume		= 2 × π2 × R × r2
		= 2 × π2 × 7 × 32
		= 2 × π2 × 7 × 9
		= 126 π2
		≈ 1244

Note: Area and volume formulas only work when the torus has a hole!

And did you know that Torus was the Latin word for a cushion? (This is not a real roman cushion, just an illustration I made)

When we have more than one torus they are called tori
 

As the small radius (r) gets larger and larger, the torus goes from looking like a Tire to a Donut: